More and more computation is being outsourced to public clouds. Cloud computers can be just as vulnerable as any other computer, putting the privacy of sensitive data at risk. As nation-state cyber weapons become increasingly available to amateur and low-level professional cyber criminals, the external threats against those cloud-based systems continue to grow. In addition, clouds are controlled by vendors who have intimate access to those machines, creating an insider threat that presents an even greater risk to privacy.
But why is privacy at risk here? Surely we’re all smart enough to encrypt our data while it’s on the move into and out of cloud-based systems. TLS, among other protocols, takes care of that for us (if we remember to use it). And surely – surely – we’re all smart enough to keep our data encrypted while at rest on these untrusted cloud servers. Right? Right? Is this microphone working? Even if we take care of both of those concerns, there’s still one unprotected attack surface: we must decrypt that data in order to compute on it, and the results of our computations still appear “in the clear” until we encrypt them. So even on our best day, privacy is at risk whenever we use the data we send to the cloud.
Could we compute on our data in the cloud while it remains encrypted? That notion sounds like science fiction. How can data that by definition is obscured to look like white noise be used for any kind of computation? Until recently, there was no good answer to that question. However, in the past few years the advent of practical homomorphic encryption (HE) and a competing technology, secure multi-party computation, promises a solution. HE carries out computation on encrypted inputs, keeps internal variables private even from observers who can look inside the running program, and produces encrypted outputs accessible only to a user who holds the right cryptographic key. HE provides security guarantees that are cryptographically as sound (and based on some of the same hard mathematical problems) as more familiar cryptography such as the block ciphers that protect our data at rest and the public key constructions that enables security in transit.
What can the cryptography community demonstrate with HE today? Voice-over-IP communications at streaming rates that don’t require a trusted central server because voice streams are never decrypted except at the receiver’s phone.1 Prototypes would be as follows: Checking encrypted files for the presence of selected strings without decrypting them. Facial recognition where facial images remain encrypted throughout the process.2 Analytics such as linear regression on encrypted data. Fast written character recognition3 with encrypted input images. Some of these prototypes are quite fast, some very slow. Simpler programs tend to perform better, but not always.
How does this seemingly magical technology work? Like all computation, it begins with a program to run and a set of choices about how secure we need the inputs, variables, and outputs of that program to be. But not every program can be transformed using HE, because such transformation requires that the program first be turned into a circuit: a collection of interconnected logic (think AND or NOT) or arithmetic (think addition and multiplication) gates. We’ll avoid descending into Galois Field theory, it’s enough to say that these circuits are either Boolean, where all values are either 0 or 1, or they are arithmetic, where values are integers. We can use those Boolean or arithmetic fields to represent many kinds of data: strings, bit vectors, integers, fixed-point numbers, and with extra work, floating-point numbers.
How can data that by definition is obscured to look like white noise be used for any kind of computation?
Many simple program statements are easy to transform into such circuits. However, things get problematic when control flow in our program is data-dependent – that is, when program flow such as loops or other conditional statements depend on the value of variables in the program rather than constants. So, although many programs and data types can be represented in HE, there are some limits.
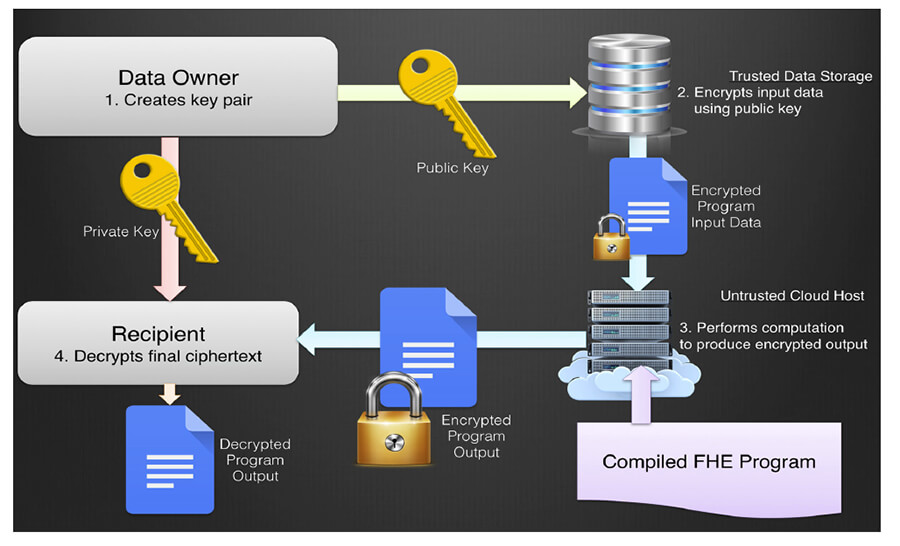
Once we have a program that we can transform into a suitable circuit, we need to encrypt the input data for the circuit. HE works because of a mathematical property called homomorphism. Roughly speaking, a homomorphism is a mapping where each element in one domain corresponds to an element in another, the same mathematical operations (addition and multiplication in our case) apply in each, and the results of those operations carry back and forth between them. Encrypting in HE is the process of mapping one domain, such as 32-bit integers, into another domain, such as integers in a very large prime modulus, in a way that preserves this homomorphism. The figure on next page shows how HE works. First, the owner of the sensitive data generates a key pair consisting of a public and a private key. Second, the owner (or a trusted repository of the sensitive data) uses the public key to encrypt the data, mapping it to the new domain. Third, an untrusted computer takes the encrypted data (which it cannot decrypt because it doesn’t get the private key) and computes the intended program on it. Fourth, the encrypted result of that computation is decrypted by whoever holds the private key.
The encryptions used for HE introduce one notable problem that explains part of the performance cost of HE: each operation in the embedded domain introduces “noise”. As information flows through each gate in our HE circuit, that noise builds up, and at some point we lose the ability to decrypt an output back into a valid plaintext. This problem originally prevented homomorphic encryption from being more than a theoretical exercise. Today, we use two approaches to prevent noise from growing too large: leveled HE schemes that can accommodate deep circuits if properly configured in advance; and bootstrapping, a process that resets noise without losing privacy. These tools give us a new capability: fully homomorphic encryption (FHE) that is usable on circuits of any depth, limited only by the user’s patience.
If FHE is so well understood, why isn’t it in broad use today? In addition to the limitations on the kinds of programs that can be transformed into circuits suitable for FHE, there are two significant limitations on FHE: user patience (by which I mean performance), and ciphertext expansion. I’ll employ here the standard automotive caution: your mileage may vary. Intuition about what makes computing slow in plaintext often offers little insight into performance in the FHE domain. However, broadly speaking, when we do math in very large fields it takes longer. In addition, it takes time to encrypt inputs into those fields, and it takes time to bootstrap when noise grows too large. Thus FHE computations can take a long time relative to their plaintext counterparts. In 2011, long time meant that such computations were either impossible, or might take up to 12 orders of magnitude as long as computing in the clear. Today, long time might mean from as little as 1000 to as much as a million times longer than computing “in the clear” – and things continue to improve. In addition to performance concerns, the encryption of data from the natural fields we compute on, such as 32-bit or 64-bit integers, into the fields used in FHE causes significant expansion: resulting ciphertexts ended up much larger than their associated plaintext. A few years ago, that expansion was typically a factor of thousands. More recently, expansion factors are closer to one order of magnitude: not trivial, but much improved.
I lied in the previous paragraph. There’s one more important limitation to broad use of FHE: making it easy to use. As you might expect, the needs to transform programs into circuits, carefully configure FHE computations, manage encryption and decryption, and other complexities make programming FHE applications the domain of a small number of expert researchers. To bring FHE into practical use, we need to integrate FHE capabilities as seamlessly as possible into existing programming environments; allow for programmers to write in the same languages to express both normal and FHE computation; automate the tedious process of converting programs into efficient circuits; make selection of the many necessary configuration parameters simple for non-experts; and transparently handle the encryption and decryption process so that from the programmer’s perspective, calling FHE-protected functions is no different from calling normal code.
For the past nine months, a joint team from Galois, Inc. and the New Jersey Institute of Technology has been researching ways to address these needs. This work, sponsored by the Intelligence Advanced Research Projects Agency (IARPA), aims to pioneer new methods in FHE ease of use and lay the groundwork for substantial further improvement. To provide seamless integration, our team built FHE capabilities into the Julia scientific programming language. To enable ease of programming, we taught the Julia compiler to generate FHE code from normal Julia functions as programmers typically write them (with a few small additions in syntax). To automate the circuit conversion process, we integrated Galois tools that use symbolic execution to automatically transform the actions of a program on variables into formulas for those variables that are then automatically expressed as circuits for FHE. We added behind-the-scenes support to handle encryption, FHE computation in the cloud, and decryption of returned results so that using FHE functions is as easy as using other Julia functions. Supporting this “front end” work was a high-value “back end”: the creation of a large, full-featured library of FHE primitives that the compiler suite calls to provide the complex mathematics needed for program execution.
Recent demonstrations of RAMPARTS results at JuliaCon and government sponsors to show how far we’ve come, and that our work continues today. Still, there’s much more to do, and our project just scratches the surface. We need standardization of library interfaces and configuration settings so that FHE can leverage the combined efforts of many library developers. We need further work in FHE cryptographic theory to reduce ciphertext expansion and improve performance. And among other things, we need to develop practical examples of applications that show how FHE can be effective and efficient in enabling secure computation on real-world problems.
The need for privacy is evident anywhere that computing on sensitive data is outsourced to untrusted computers like those in modern clouds. The risk of losing that privacy continues to grow as cyber threats grow both more numerous and more sophisticated. Even on our best day, we still expose data to those threats at least long enough to compute on it – too long to avoid compromise. FHE offers one way to secure that privacy by computing on data while it remains encrypted. There’s still some way to go before FHE can be ubiquitous: we need better performance and a significant focus on ease of use. But then every gig economy is driven by new technology. Hey, can you give me a Lyft to my AirBnB? And do you take Bitcoin?
Sources
- Archer, David W., and Kurt Rohloff. “Computing with data privacy: Steps toward realization.” IEEE Security & Privacy 13, no. 1 (2015): 22-29.
- Troncoso-Pastoriza, J.R., González-Jiménez, D. and Pérez-González, F., 2013. Fully private noninteractive face verification. IEEE Transactions on Information Forensics and Security, 8(7), pp.1101-1114.
- Nathan Dowlin, Ran Gilad-Bachrach, Kim Laine, Kristin Lauter, Michael Naehrig, and John Wernsing. 2016. CryptoNets: applying neural networks to encrypted data with high throughput and accuracy. In Proceedings of the 33rd International Conference on International Conference on Machine Learning – Volume 48 (ICML’16), Maria Florina Balcan and Kilian Q. Weinberger (Eds.), Vol. 48. JMLR.org 201-210.
David W. Archer, PhD



Leave a Comment